| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 신경망
- 백준
- OpenGL
- 컴퓨터 비전
- Support Vector Machine
- C++
- 인공지능
- Kaggle
- SGD
- 딥러닝
- recommender system
- 그래픽스
- Computer Vision
- petal to metal
- 비용함수
- cs231n
- Vision
- 컴퓨터 그래픽스
- Unsupervised learning
- SVM
- 로지스틱 회귀
- pre-trained
- CNN
- Regularization
- 파이썬
- neural network
- 추천 시스템
- logistic regression
- CPP
- 머신러닝
- Today
- Total
kwan's note
좌표계 변환 (transform and rotation) 본문
좌표계 변환 (transform and rotation)
kwan's note 2021. 6. 24. 20:37본 학습노트는 2021년 1학기 고려대학교 한정현 교수님의 컴퓨터 그래픽스 강의를 수강하고 작성하였습니다.
https://reminder-by-kwan.tistory.com/132
모델링, vertex array 와 index array
본 학습노트는 2021년 1학기 고려대학교 한정현 교수님의 컴퓨터 그래픽스 강의를 수강하고 작성하였습니다. https://reminder-by-kwan.tistory.com/131 컴퓨터 그래픽스 서론 본 학습노트는 2021 1학기 고려
reminder-by-kwan.tistory.com
2차원에서의 scaling과 rotation을 먼저 보자.
간단하게 행렬로 표현하면 다음과 같다.
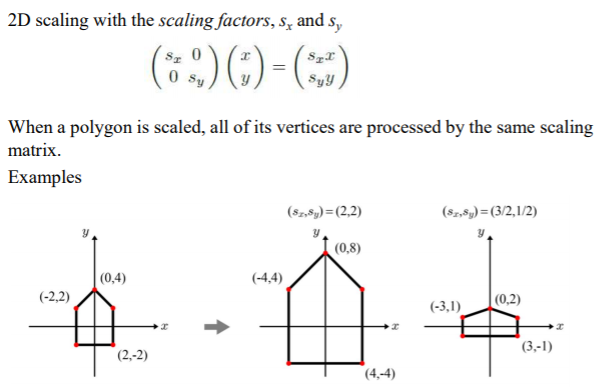
다음으로 2차원 회전은 다음과 같다.
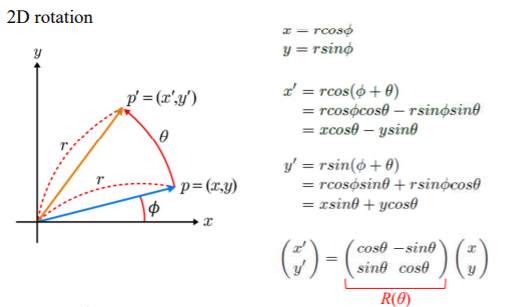
2차원 선형변환에 대한 이론적 내용은 위키피디아를 참조
https://ko.wikipedia.org/wiki/%EC%84%A0%ED%98%95_%EB%B3%80%ED%99%98
선형 변환 - 위키백과, 우리 모두의 백과사전
선형대수학에서, 선형 변환(線型變換, 영어: linear transformation) 또는 선형 사상(線型寫像, 영어: linear map) 또는 선형 연산자(線型演算子, 영어: linear operator) 또는 선형 작용소(線型作用素)는 선형
ko.wikipedia.org
지금까지 본 확대/ 축소와 회전은 선형변환이다. 하지만 이동(translation)은 선형 변환이 아니므로 위와 같은 행렬의 곱으로 표현할 수 없다. 선형 변환과 달리 이동은 일반적으로 행렬의 덧셈으로 표현되는데
동차좌표(homogeneous coordinate)를 이용하면 행렬곱으로 나타낼 수 있게된다.

실제 곱해봄으로서 간단하게 증명할 수 있다.(엄밀한 증명은 아닐지라도)
이제 여러 변환들을 행렬의 곱으로 표현할 수 있다.
어떤 점 (x,y)에 대해 변환1 (M1) 변환2(M2)를 하고 싶다면 M2*M1*(x,y)T 로 표현하면 된다.
(column vector 표현으로 하자)
이때 M2 와 M1의 곱은 하나의 행렬로 표현될 수 있다.

이러한 변환을 affine transform (아핀변환)이라고 한다. 아핀변환은 선형변환과 이동을 포함하는 변환이다.
n차원 아핀변환은 n+1차원의 행렬로 표현되므로 2차원 변환은 3x3 행렬로 표현된다.
이제 3차원을 보도록 하자.
3차원에서의 scaling도 2차원에서와 동일하다.
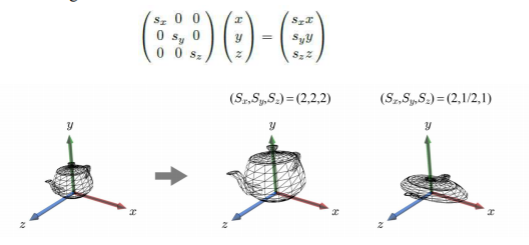
행렬의 대각성분을 scaling 해주면된다.
회전의 경우 2차원과 조금 다르게 표현되는데 2차원에서는 회전이 원점을 기준으로 반시계 방향으로 표현되는데
3차원의 경우 다양한 회전축 표현이 가능해진다.
대표적으로 x축회전을 보자.

x축을 기준으로 회전하는 주전자가 어떤 방식으로 회전하는지 직관적으로 알 수 있다.
y축 회전의 경우 Ry = mat3({cos,0,sin},{0,1,0},{-sin,0,cos}) 으로 표현된다.
2차원과 마찬가지로 ccw의 경우 양수로 표현되고 cw는 음수로 표현할 수 있다.
이제 translation을 보도록 하자.
2차원과 마찬가지로 affine transform의 경우 n+1 차원 행렬을 통해 표현할 수 있다.
만약 점(x,y,z)에 대해서 (dx,dy,dz)만큼 이동을 하고싶다면 다음과 같은 표현으로 이동할 수 있다.

이제 이러현 변환을 어디에 사용하는지 알아보자. 물론 변환 행렬은 물체를 이동하고 변형시키는 많은곳에 사용될 수 있지만 가장 대표적인 하나의 과정은 world transform이다.
물체를 모델링하는데 사용하는 공간을 object space라고 하는데 이 object space는 개별 물체를 정의하는 공간이므로 실제로 표현하고자 하는 스크린의 이미지를 모두 표현할 수 없다. 즉 개별 물체가 존재하는 공간을 object space라고 하고 표현하고싶은 world가 존재하는 공간을 world space라고 하기 때문에
우리는 world transform을 통해 object space에 정의되었던 물체들을 world space로 변환시켜야 한다.
이러한 변환을 world transform이라고 한다.

이런 4x4 affine transform에 있어서 항상 네번째 행은 (0,0,01)T이다.
나머지 3x4행렬은 L|T로 표현되는데 왼쪽을 accumulated linear transform
오른쪽을 accumulated translation으로 볼 수 있다.
다만 이때 L는 T의 영향을 받지 않지만 T은 L의 영향을 받게된다. [L|T]로 변환된 행렬을 보면 L을 먼저 계산하고 T를 계산한것으로 볼 수 있다. 즉 linear transform을 먼저 진행하고 translation한 형태가 된다.
world transform의 결과는 object space를 world space에 맞추는것으로 볼 수 있다. 즉 물체는 자신의 object space와 일치하게되어 거동한다. {e1,e2,e3}는 world space 의 basis를, {u,v,n}은 object space의 basis를 나타낸다고 하면 world transform 이후 E=u,v,n가 된다. 하지만 이후 물체를 회전시키면 world 공간의 basis u,v,n은 그대로 유지되나 물체 공간의 basis {e1,e2,e3}는 회전한다.
이때 회전을 R이라고 하자. 회전 후 basis는 다음과 같이 변한다.

'graphics VR AR > Computer Graphics -Korea Univ' 카테고리의 다른 글
| 래스터라이저 (Rasterizer) (0) | 2021.06.25 |
|---|---|
| 정점 처리 ( view transform, projection transform) (0) | 2021.06.24 |
| 모델링, vertex array 와 index array (0) | 2021.06.24 |
| 컴퓨터 그래픽스 서론 (0) | 2021.06.24 |
| 컴퓨터 그래픽스 복습노트 (0) | 2021.06.24 |




