| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- neural network
- 로지스틱 회귀
- petal to metal
- SVM
- OpenGL
- Regularization
- 컴퓨터 그래픽스
- 머신러닝
- cs231n
- Kaggle
- recommender system
- Support Vector Machine
- CPP
- 컴퓨터 비전
- CNN
- pre-trained
- 추천 시스템
- 그래픽스
- logistic regression
- Unsupervised learning
- 비용함수
- 딥러닝
- Computer Vision
- C++
- Vision
- SGD
- 백준
- 파이썬
- 인공지능
- 신경망
- Today
- Total
kwan's note
linear classification, SVM - 선형 분류 본문
출처 : cs231n lecture2
www.youtube.com/watch?v=OoUX-nOEjG0&list=PLC1qU-LWwrF64f4QKQT-Vg5Wr4qEE1Zxk&index=2
linear classification은 매우 기본이 되는 분류 방식이다. neural network의 근간이 되는 분류 방식이기도 하다.
linear classification은 특징들이 parameter 형식으로 요약되어서 그 내적의 결과가 결과로 나타나는 방식이다.
parametric approach를 보도록 하자. input으로 이미지를 넣으면 어떠한 계산을 진행하고 그 걸과로 값들을 반환받는다. 이때 반환값은 각 클래스의 점수가 되는데 해당점수가 가장 높은 클래스를 이미지의 클래스로 선택하게 된다.

이미지를 2X2로 매우 단순화시켜서 생각해 보도록 하자. 이 이미지를 3가지 클래스중 하나로 나누려고 할 때 아래와 같은 연산을 거쳐 점수가 가장 높은것을 선택한다.


CIFAR10에서 선형분류를 하고 해당 classifier를 시각화하였을때 보면 위 이미지와 같다.
학습에서 얻은 행렬W의 열은 각픽셀이 결과에 얼마나 영향을 미치느냐를 나타낸다. 위 이미지는 이 열들을 unravel하여 이미지로 나타낸 것이다.
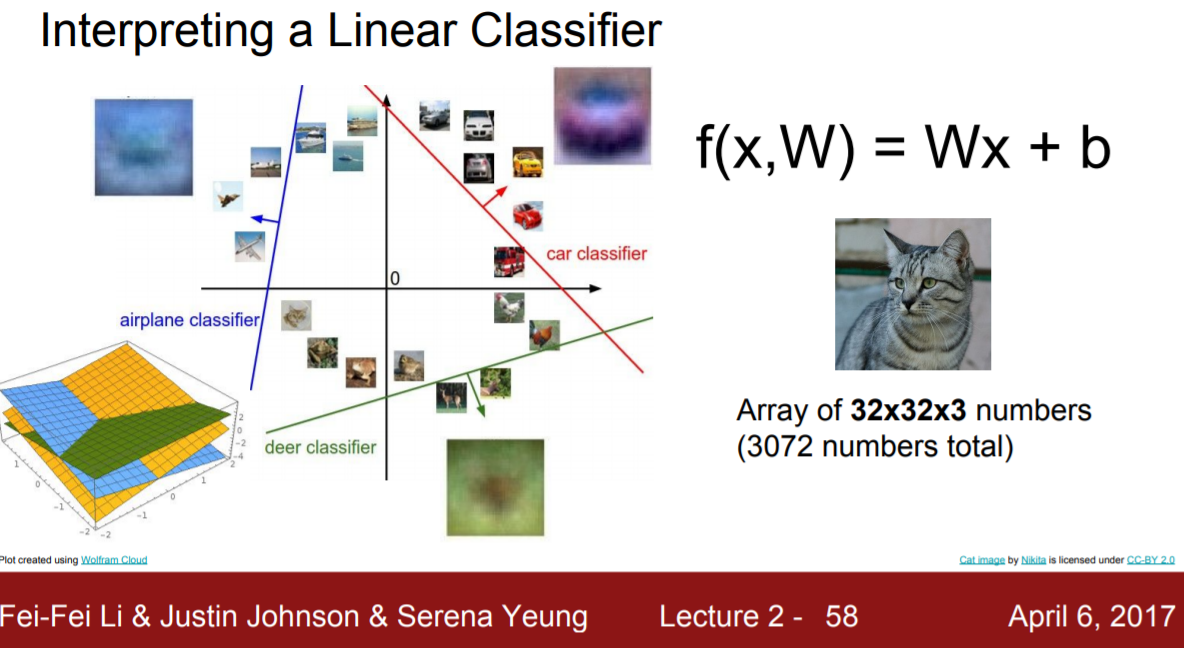
그렇다면 이제 함수 f를 어떻게 정하는지 알아보도록 하자.
우리는 어떤 W가 가장 올바른 결과(가장 덜 틀린 결과)를 가져다줄지 파악해야 한다.
즉 W를 평가하는 방법을 생각해보도록 하자.

mulitclass SVM loss는 다음과 같다.
Syi 즉 올바른 값이 각 값에 1을 더한것보다 클 때 Li=0이다. 그렇지 않다면 Sj-Syi+1을 Li값에 더한다.
총 sum이 Loss 값이 된다.
아래 3class 예시를 보자.

위와 같이 점수를 계산하여 합하는 방식으로 W의 타당성을 판단한다.
+1을 하는 이유는 모든 class 의 점수가 같을때도 (즉 정상적인 판단을 하지 못하였을 때도) loss function의 값이 0이 되기 때문에 이를 방지하고자 margin을 추가한 것이다.
이 기준을 가지고 train example 에서 loss function을 최소로 하는 W를 계산하여 결과값을 얻는다.
하지만 여기서는 Li가 0인경우 W값이 두배가 되더라도 동일하게 0을 얻는다. 그리고 W는 유일하지 않게된다.
따라서 다음 강의에서는 다른 분류 방법인 softmax 를 이용한 방법에 대해 소개하도록 하겠습니다.
reminder-by-kwan.tistory.com/116
linear classification with softmax - 소프트맥스 회귀
출처 : cs231n lecture3 www.youtube.com/watch?v=h7iBpEHGVNc 이번에는 저번시간에 이어서 linear classification의 방식에 대해 알아보도록 하겠습니다. reminder-by-kwan.tistory.com/115 linear classificatio..
reminder-by-kwan.tistory.com
'computer vision > cs231n-Stanford' 카테고리의 다른 글
| Backpropagation -역전파 (0) | 2021.02.14 |
|---|---|
| linear classification with softmax - 소프트맥스 회귀 (0) | 2021.02.14 |
| k nearest neighbor - k 최근접 이웃 (0) | 2021.02.14 |
| cs231n (0) | 2021.02.13 |



