선형독립과 선형종속(Linear Independence and Linear Dependence)

출처: 부스트코스-인공지능을 위한 선형대수

수강일시:2021.01.05

 

선형독립의 정의1.

span의 증가여부로 판단하는 정의(practial definition)

벡터를 하나씩 넣으면서 span을 지속적으로 증가시켜주는경우에만 선형 독립으로 본다.

만약 span을 넓히지 않는다면 선형 종속으로 본다.

 

추가)

하지만 전체 차원이 정해진경우 ex)3차원공간내에서 4개의 벡터가 존재한다면 최소한 한쌍의 벡터는 선형 종속이 된다.

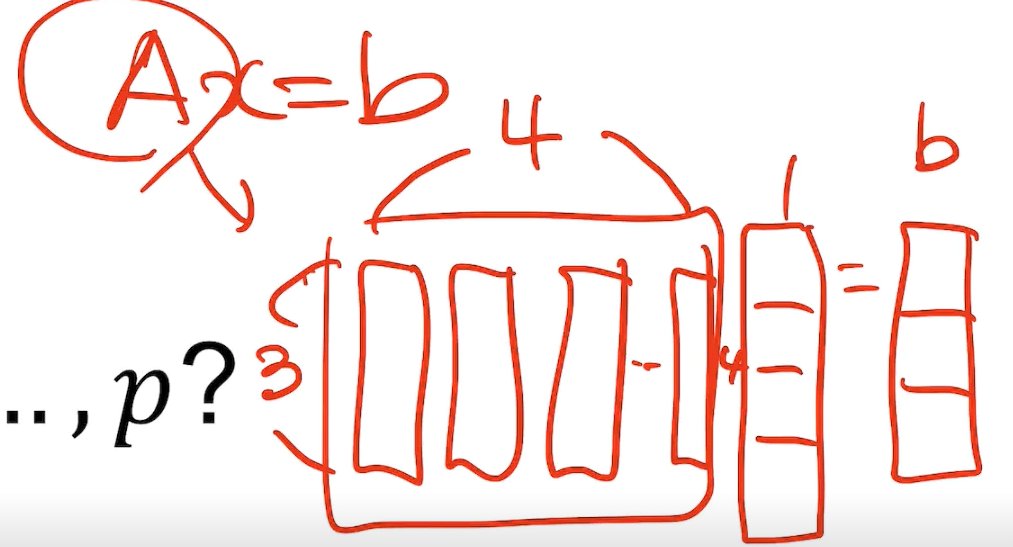
Ax =b 라는 방정직으로 보고 A를 3X4행렬로 보는경우가 이에 해당한다.

즉 미지수의 갯수보다 방정식의 갯수가 적으면 무수히 많은 해가 존재한다.

 

 

 

 

 

 

정의2. formal definition

homogeneous equation에 대해 x1 ... xn =0 인 trivial solution을 제외한 해가 존재한다면 independent하다