반응형
Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- logistic regression
- OpenGL
- 컴퓨터 비전
- 파이썬
- Vision
- Unsupervised learning
- SVM
- pre-trained
- 인공지능
- petal to metal
- 추천 시스템
- 딥러닝
- 그래픽스
- 비용함수
- 머신러닝
- SGD
- Support Vector Machine
- CNN
- Computer Vision
- Regularization
- 로지스틱 회귀
- cs231n
- recommender system
- CPP
- neural network
- C++
- 신경망
- 컴퓨터 그래픽스
- Kaggle
- 백준
Archives
- Today
- Total
kwan's note
그람-슈미트 직교화(Gram-Schmidt Orthogonalization) 본문
반응형
출처: 부스트코스-인공지능을 위한 선형대수
수강일시:2021.01.07
linearly independent하지만 orthogonal 하지는 않은 factor들에 대해 직교화를 통해 영향을 주지 않도록 만들고자 한다. 이러한 방식을 직교화라고 하는데 이 장에선 그람슈미트 직교화 방법에 대해 공부하고자 한다.

[3 6 0] dot [1 2 2] != 0
normalize x1 =v1= [3/sqrt(45) 6/sqrt(45) 0]T
x2와 v1의 내적 = 15/sqrt(45)
v2' = x2- 15/sqrt(45) * v1 =[0 0 2]T
normalize v2' = v2=[0 0 1]T
v1 v2를 이용해 어떠한 matrix를 곱해 원래 벡터 x1 x2를 만들고자 한다.


v1은 x1을 normalize 한 것이므로 1번에는 sqrt(45) 2번에는 0이 된다.
v2는 x2를 사영에 x1을빼고 normalize 한 것이었다.
따라서 1의 오른쪽에는 15/sqrt(45) 2의 오른쪽에는 2가 된다
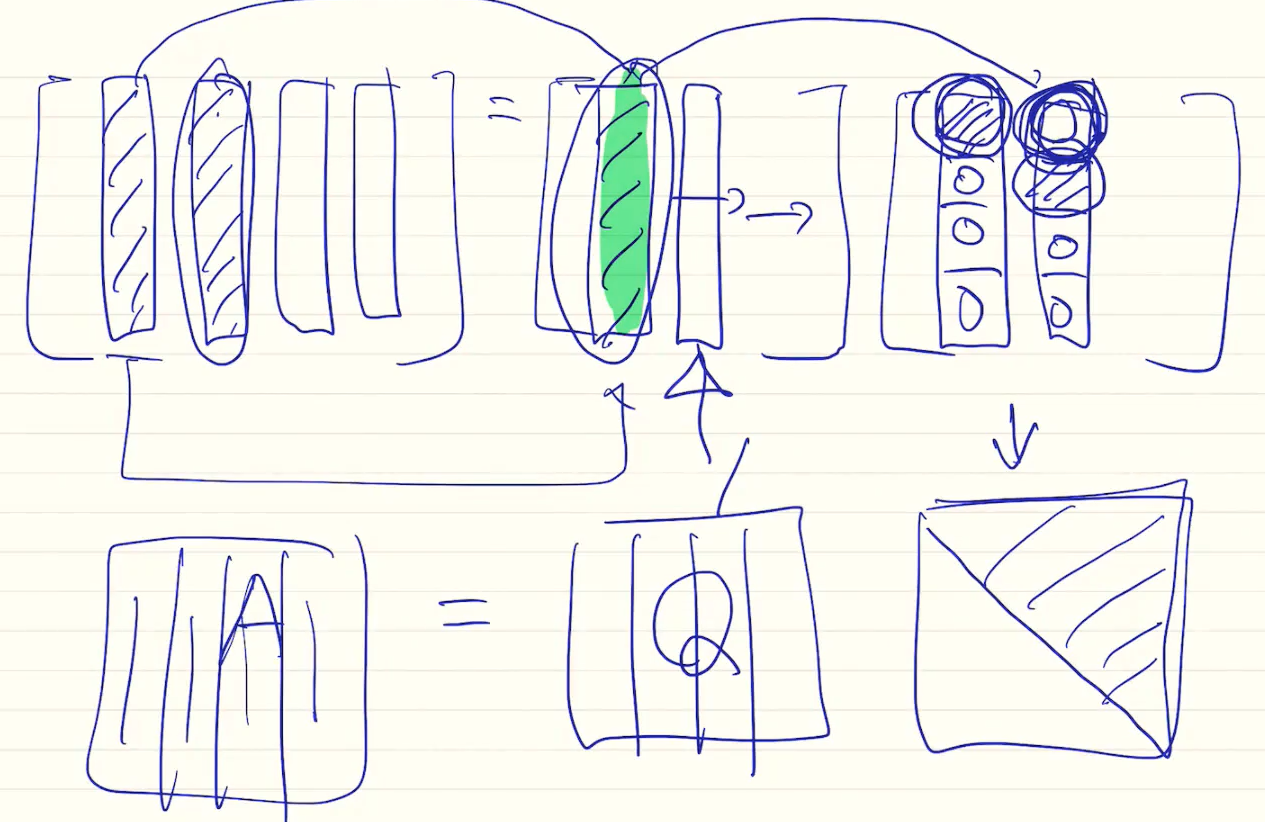
두개가 아닌 여러 column이 있을때 Q의 첫번째 column은 normalize 한 계수로 1행이채워지고 나머지는 0이된다
두번째행은 첫번째에 사영하고 normalize했으므로 두개행만채워진다
... 이러한 방식으로 채워나가면 곱하는 행렬이 위쪽삼각행렬이 된다.
반응형
'Math > Linear algebra' 카테고리의 다른 글
| 영공간(Null Space)과 직교여공간(Orthogonal Complement) (0) | 2021.01.07 |
|---|---|
| 고유벡터와 고유값 (Eigenvectors and eigenvalues) (0) | 2021.01.07 |
| 정사영 (Orthogonal Projection) (0) | 2021.01.07 |
| 정규방정식 (0) | 2021.01.06 |
| 최소제곱 문제(Least Squares Problem) (0) | 2021.01.06 |




