| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- recommender system
- Support Vector Machine
- SGD
- petal to metal
- 백준
- CNN
- Vision
- 인공지능
- 추천 시스템
- CPP
- OpenGL
- Unsupervised learning
- C++
- 그래픽스
- SVM
- 파이썬
- 딥러닝
- 컴퓨터 비전
- cs231n
- Kaggle
- 로지스틱 회귀
- logistic regression
- Regularization
- pre-trained
- 머신러닝
- 비용함수
- 신경망
- neural network
- Computer Vision
- 컴퓨터 그래픽스
- Today
- Total
kwan's note
cost function in logistic regression -로지스틱 회귀에서 비용함수 본문
cost function in logistic regression -로지스틱 회귀에서 비용함수
kwan's note 2021. 1. 26. 18:17출처: machine learning by andrew ng, stanford cousera lecture
수강일시: 2021.01.26
reminder-by-kwan.tistory.com/91
logistic regression -로지스틱 회귀
출처: machine learning by andrew ng, stanford cousera lecture 수강일시: 2021.01.26 reminder-by-kwan.tistory.com/86 supervised learning -지도학습 출처: machine learning by andrew ng, stanford cousera..
reminder-by-kwan.tistory.com
로지스틱 회귀에서 비용함수를 생각해보자.
이전까지는 비용함수를 h-y의 제곱에 비례하는 수로 정의했다. 이를통해 h와 y의 거리를 구했고 그 제곱의 합을 최소화 하는 방법으로 classification을 진행했는데 이를 진행하다보면 단점이 존재한다.
그중 가장 큰 단점으로는 최소제곱합 방식의 비용함수는 non convex function이 된다는것이다.
오목함수가 되지 않는다면 이전에 배웠던 gradient descent 즉 경사하강법을 사용할 수 없다.

따라서 이제 로지스틱회귀에서는 새로운 costfunction을 정의해서 사용하고자 한다.

새로운 cost function은 로그함수를 사용해서 정의한다. y=1이고 h=1일때 cost가 0이되고 y=0 h=0일때도 cost가 0이되는것을 확인할 수 있다. 여기서 더 나아가 자세히 살펴보도록 하자.
새로운 cost function을 도식화 하면 아래와 같다.

위 식을 간단하게 바꾸면 아래와 같이 된다.
Cost(hθ(x),y)=−ylog(hθ(x))−(1−y)log(1−hθ(x))
따라서 전체 costfunction은 아래와 같다.
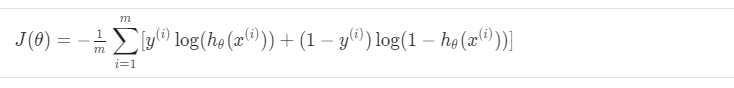
이제 위식을 이용해 gradient descent 방식으로 minimize하여 원하는 classification문제를 해결할 수 있다.

'ML and AI > Machine learning - Andrew Ng' 카테고리의 다른 글
| regularization - 정규화 (0) | 2021.01.27 |
|---|---|
| overfitting- 과적합 (0) | 2021.01.26 |
| logistic regression -로지스틱 회귀 (0) | 2021.01.26 |
| Normal Equation-정규방정식 (0) | 2021.01.26 |
| gradient descent(경사하강법) (0) | 2021.01.24 |




